How Quantum Computers Work (Oversimplified, No Complex Math)

As a software engineer of 15 years, I was very interested in how exactly quantum computers worked.

However, I couldn’t find a great explanation of quantum computers online, so I decided to create my own guide. One that wasn’t dead wrong or so filled with such complex math that no regular person could understand it.

Quick disclaimer: I’m a software engineer and blogger. My understanding of quantum mechanics leaves a lot to be desired. This is meant to be an extremely high-level overview; if you’re looking for more than that, I suggest asking questions on StackExchange.

Classical Computers vs. Quantum Computers

A classical computer uses a series of bits to describe information and instructions. We usually refer to bits as representative of 1’s or 0’s. But, we could just as easily use any binary system to describe the value of a bit. So 1 or 0, true or false, heads or tails, etc.

Let’s use heads and tails for this example (because it will make it easier to understand quantum bits later).

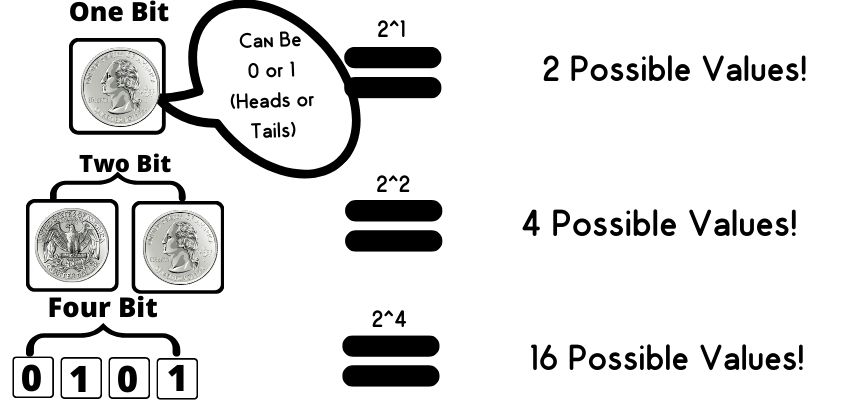
That’s the gist of how a classical computer stores data and instructions. Quantum computers are extremely similar, the difference is they leverage three quantum properties that makes them special. Let’s learn about those three properties!

#1) Wave/Particle Duality (Probability Waves)

Quantum objects (like a photon) travel through space as a probability wave until they are “observed” (interact with matter). At which point the probability wave collapses and the photon becomes a particle with a definite position in space and time.

That may be common knowledge to you if you’re familiar with quantum mechanics. Or it probably sounds like non-sense if you’re not. If this is a new subject for you I suggest watching a video on the double slit experiment to familiarize yourself with how this works.

A quantum bit (qubit) also acts as a probability wave until “observed.” You can think of a quantum bit like a spinning quarter (pre-observation) as opposed to a classical bit that always has a definitive value.

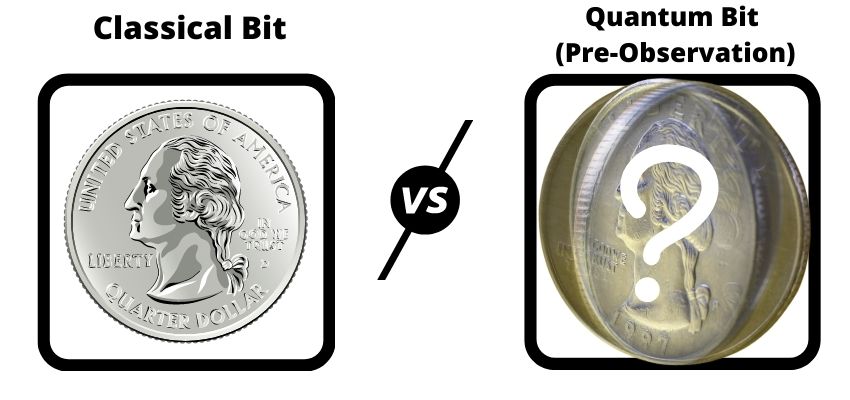
Post-observation, the quantum bit transforms into a classical bit. It obtains a definitive heads or tails value and effectively becomes no different than a classical bit post-observation.

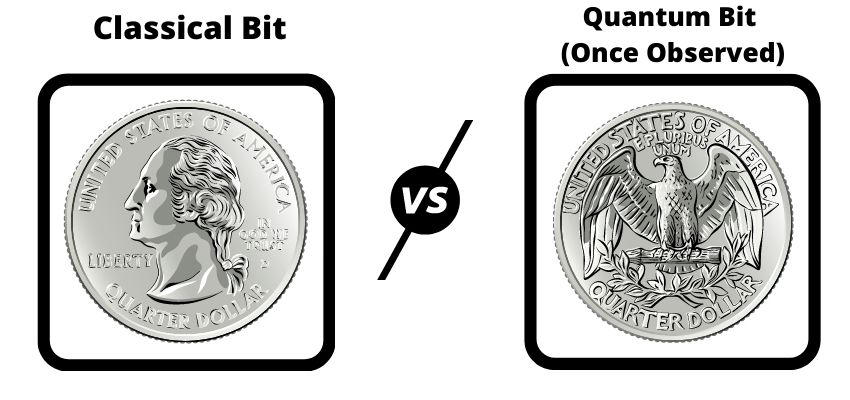
We’ll get to why this property is essential for quantum computing later. For now, Quantum Mechanics concept #2!

#2) Quantum SuperPosition

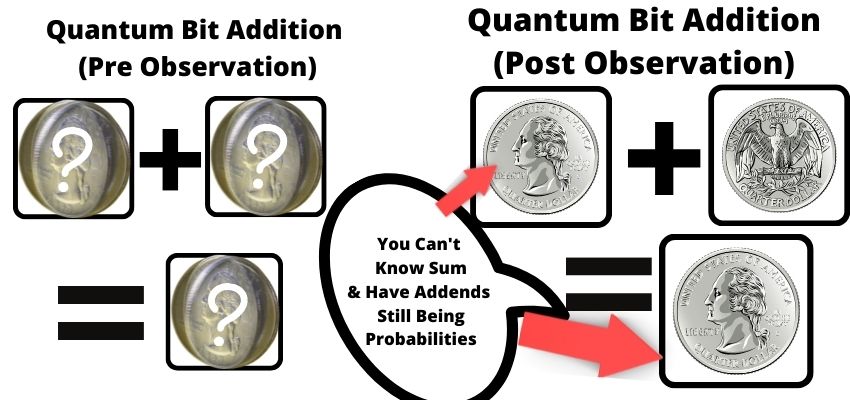
If you add two quantum bits together, the result becomes a new quantum state (probabilistic in nature, until observed). That’s quantum superposition.

If we add two bits together with classical computers, we’ll get a definitive result. But, when a quantum computer adds two qubits together, we get a 3rd probabilistic quantum state dependent on the addends.

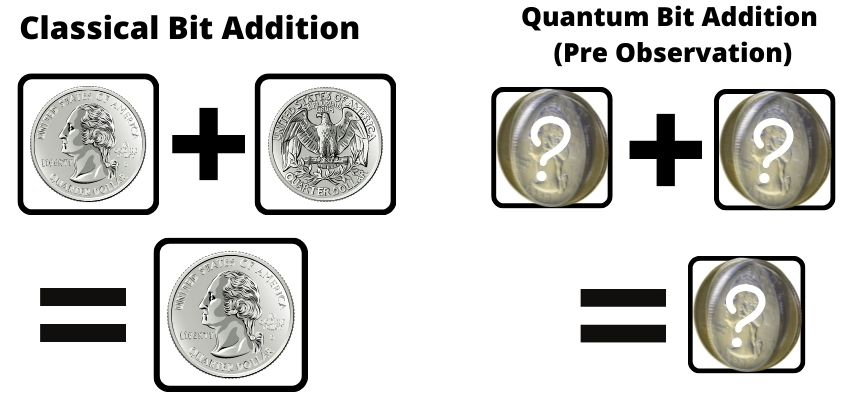
One more concept before we get to why this is valuable!

#3) Quantum Entanglement

Quantum entanglement is the idea that the quantum states that you added are linked together. Meaning if you observe the sum (the result of adding two quantum bits), then the entire probability wave collapses, and the addends automatically get actual values too. The whole system will go back to behaving like a classical computer once observed.

Note: This is all you need to know. Quantum mechanics is way more complicated than this for two reasons (You don’t need to know this, it’s just cool).

1) The probabilities of quantum bits don’t have to be 50/50

Odds of each bit can be set to anything (as long as they add to 100). See this excellent video by Veritasium to understand how we can set the probability of a quantum bit.

2) The probabilities of quantum bits are calculated using complex numbers

The math behind quantum probability uses complex numbers (imaginary numbers). This means the spinning quarters analogy I gave you is overly simplistic. You would need to use vector math to calculate probabilities instead (which is much harder). If you’re interested in this subject, see this fantastic video by Science Asylum on how the quantum wave function works.

Why does the quantum wave function behave in this strange way?

Scientists aren’t 100% certain. There are many weird interpretations of quantum mechanics derived from this complex math. The leading theory is the Copenhagen interpretation (universe splits into all probabilistic outcomes then collapses back). Still, there’s also crazy stuff like The Many World’s hypotheses (universe splits into all probabilistic outcomes and doesn’t collapse back).

The good news is we don’t need to answer these things to understand quantum computers.

Why Are Quantum Computers Better Than Classical Computers?

By now, you’re probably wondering how a bunch of probabilistic bits are better than a classical computer. Well, for most computing problems, quantum computers aren’t any better!

For instance, pretend we wanted to represent the letter ‘A’ in bits. Probabilistic bits don’t help with that task! In fact, they’d be quite detrimental. And if you think about it, most computing problems require definitive values. Meaning it’s rare that a quantum computer would come in handy for most computing tasks.

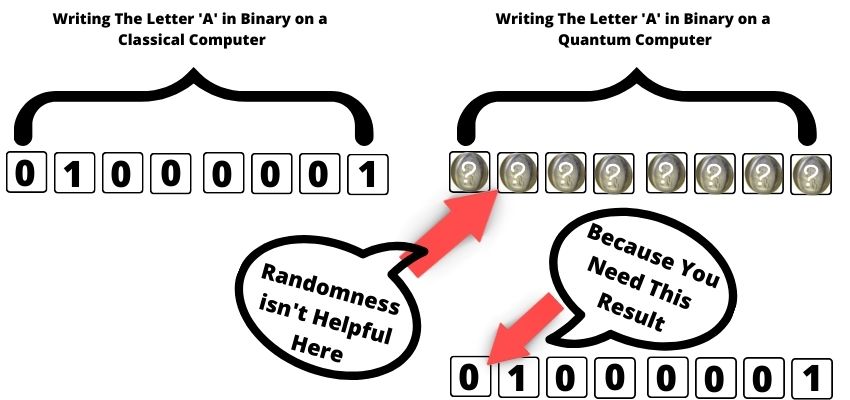
Then why do we say quantum computers will do insane things like break all internet encryption and potentially cure cancer one day?

It has to do with the computer science concept of P vs. NP. This is where we ask if every problem that can be easily verified can also be easily solved. A problem that can be solved quickly is solved in polynomial time (P). And problems that increases exponentially as you grow is solved in nondeterministic polynomial time (NP).

Below is an excellent video on the subject that can explain it better than I ever could (if you need a refresher on the subject).

The only place quantum computers beat classical computers is when we can leverage a Quantum Algorithms to solve a current NP problem in P time. That’s it. I don’t want to understate how big a deal this is (because it’s a huge deal for specific applications). But, I also need you to understand that this is all that quantum computers are good for.

So what the heck is a quantum algorithm, and how does that work?

Quantum Algorithms

The most commonly cited examples of quantum algorithms are Shor’s Algorithm, Deutsch–Jozsa algorithm, Grover’s algorithm, etc. And I’d be willing to bet many more quantum algorithms get invented or become mainstreamed as quantum computing resources become widely available.

If you’re wondering how quantum algorithms work, Minute Physics made the amazing video below specifically about Shor’s Algorithm. It explains this much more clearly than I could. I’m just going to give you the oversimplified version.

The simple explanation is that quantum algorithms are designed to exploit the probability waves’ constructive and destructive interference patterns. This allows the algorithm to brute-force the answer in fewer steps (to the point where an NP problem becomes a P problem). How does this work?

When a wave collides with another wave their amplitudes will either add together or cancel each other out.

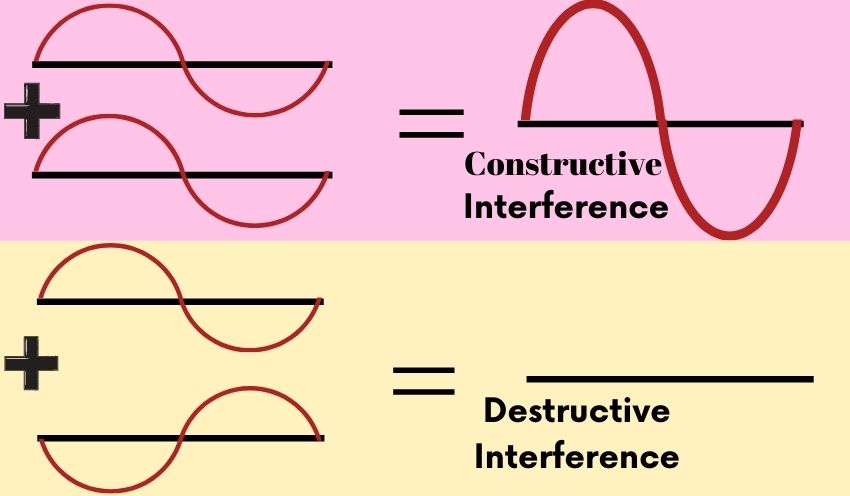
As we discussed previously, when we add quantum bits, we’re effectively adding two probability waves. These bits will naturally produce interference patterns (since qubits are composed of probability waves). Those interference patterns can significantly reduce the number of calculations needed to solve the problem.

What People Get Wrong About Quantum Computers

Many articles online say crazy things like the following.

• 100 qubits added together can hold more data than atoms in the universe (they can’t).
• A quantum computer can process tons of classical states in parallel (it can’t).
• Lots of other non-sense.

At the end of the day, a quantum bit transforms into a classical bit once observed. Meaning you should be incredibly skeptical if you read wild claims on the Internet about what quantum computers can do.

Well, unless it involves transforming an NP problem into a P problem using a quantum algorithm. Quantum computers can theoretically do that (sometimes).

What’s the Largest Quantum Computer In Existence Right Now?

Quantum computers have moved beyond the theoretical, and many already exist. Right now (Dec 2021), Honeywell (built by IBM) claims to have the largest number of reliable Qubits at 64. But, this is increasing all the time, and it will likely seem like an extremely small number of qubits in a few years.

The problem quantum computers have is that 64 bits isn’t very many bits. This blog post alone was a 300 KB download (37,500 times larger). As such, we’ve probably got a few years before quantum computers are breaking internet encryption. We need orders of magnitude more qubits before the quantum party starts.

Will You Ever Own a Quantum Computer

You will never own a quantum computer.

The first classical computer to debut in the US weighed 29,000 lbs (UNIVAC I in 1951). At the time, something like an iPhone would have been unimaginable (only 56 years later).

That said, quantum computers have a physics problem! When quantum bits interact with the classical world, they become classical bits. This is why quantum computers currently reside in magnetically sealed vacuum chambers operating at near absolute zero temperatures. We STILL have significant problems with decoherence (errors due to interference from the outside world) despite this.

I genuinely don’t understand how it’d be possible to overcome that minus a dramatic leap in technology. But, even if we could, there’s no point to you owning a quantum iPhone. Quantum computers are specialized machines meant to solve very specific NP problems, not perform classical computing tasks.

That said, I could easily see quantum computing resources becoming available via the cloud (Nothing is stopping us from hooking one to the Internet). In that sense, you might be able to buy time on a quantum computer in the near future.